MATLAB Examples 2 (covering Statistics Lectures 3 and 4)
Contents
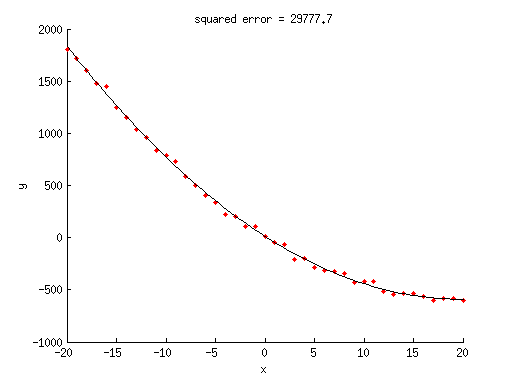
Example 1: Fit a linearized regression model
% generate some random data x = -20:20; y = 1.5*x.^2 - 60*x + 10 + 30*randn(size(x)); % given these data, we will now try to fit a model % to the data. we assume we know what model to use, % namely, y = ax^2 + bx + c where a, b, and c are % free parameters. notice that this was the model % we used to generate the data. % since our model is a linearized model, we can express % it using simple matrix notation. % construct the regressor matrix X = [x(:).^2 x(:) ones(length(x),1)]; % estimate the free parameters of the model % using ordinary least-squares (OLS) estimation w = inv(X'*X)*X'*y(:); % what are the estimated weights? w
w =
1.5368275257135
-60.638944801903
8.15661270608602
% what is the model fit? modelfit = X*w; % what is the squared error achieved by this model fit? squarederror = sum((y(:)-modelfit).^2); % visualize figure; hold on; scatter(x,y,'r.'); ax = axis; xx = linspace(ax(1),ax(2),100)'; yy = [xx.^2 xx ones(length(xx),1)]*w; plot(xx,yy,'k-'); xlabel('x'); ylabel('y'); title(sprintf('squared error = %.1f',squarederror));
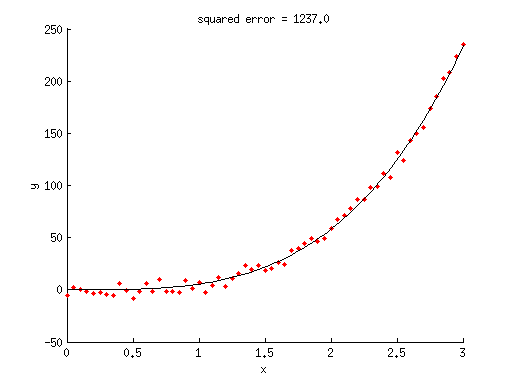
Example 2: Fit a parametric nonlinear model
% generate some random data x = 0:.05:3; y = 5*x.^3.5 + 5*randn(size(x)); % given these data, we will now try to fit a model % to the data. we assume we know what model to use, % namely, y = ax^n where a and n are free parameters. % notice that this was the model we used to generate the data. % define optimization options options = optimset('Display','iter','FunValCheck','on', ... 'MaxFunEvals',Inf,'MaxIter',Inf, ... 'TolFun',1e-6,'TolX',1e-6); % define bounds for the parameters % a n paramslb = [-Inf 0]; % lower bound paramsub = [ Inf Inf]; % upper bound % define the initial seed % a n params0 = [ 1 1]; % estimate the free parameters of the model using nonlinear optimization % hint: pp is a vector of parameters like [a n], % xx is a vector of x-values like [.1 .4 .5], % and what modelfun does is to output the predicted y-values. modelfun = @(pp,xx) pp(1)*xx.^pp(2); [params,resnorm,residual,exitflag,output] = lsqcurvefit(modelfun,params0,x,y,paramslb,paramsub,options);
Norm of First-order
Iteration Func-count f(x) step optimality CG-iterations
0 3 431921 7.93e+03
1 6 431921 10 7.93e+03 0
2 9 247013 2.5 8.3e+04 0
3 12 247013 2.81299 8.3e+04 0
4 15 98286.2 0.703246 1.09e+05 0
5 18 17315.7 1.40649 3.78e+05 0
6 21 1894.05 0.327179 2.46e+04 0
7 24 1482.46 0.939262 9.09e+03 0
8 27 1241.08 0.422605 1.33e+03 0
9 30 1237.01 0.00758631 5.5 0
10 33 1237.01 1.29563e-05 7.82e-05 0
Local minimum possible.
lsqcurvefit stopped because the final change in the sum of squares relative to
its initial value is less than the selected value of the function tolerance.
% what are the estimated parameters?
params
params =
5.4338041940236 3.42528833322854
% what is the model fit? modelfit = modelfun(params,x); % what is the squared error achieved by this model fit? squarederror = sum((y(:)-modelfit(:)).^2); % (note that the 'resnorm' output also provides the squared error.) % visualize figure; hold on; scatter(x,y,'r.'); ax = axis; xx = linspace(ax(1),ax(2),100)'; yy = modelfun(params,xx); plot(xx,yy,'k-'); xlabel('x'); ylabel('y'); title(sprintf('squared error = %.1f',squarederror));
Example 3: Another optimization example
% generate some random data x = rand(1,1000).^2; % we want to determine the value that minimizes the sum of the % absolute differences between the value and the data points % define some stuff options = optimset('Display','iter','FunValCheck','on', ... 'MaxFunEvals',Inf,'MaxIter',Inf, ... 'TolFun',1e-6,'TolX',1e-6); paramslb = []; % [] means no bounds paramsub = []; params0 = [0]; % perform the optimization % hint: here we have to apply a square-root transformation so that when % lsqnonlin squares the output of costfun, we will be back to absolute error. costfun = @(pp) sqrt(abs(x-pp)); [params,resnorm,residual,exitflag,output] = lsqnonlin(costfun,params0,paramslb,paramsub,options);
Norm of First-order
Iteration Func-count f(x) step optimality CG-iterations
0 2 346.47 500
1 4 346.385 8.61928e-05 490 0
2 6 341.862 0.00491093 440 0
3 8 333.538 0.0101418 387 0
4 10 315.811 0.0259447 306 0
5 12 308.364 0.0129775 271 0
6 14 292.776 0.0324211 215 0
7 16 279.22 0.035143 170 0
8 18 270.08 0.0314543 118 0
9 20 263.724 0.031138 88 0
10 22 259.555 0.0265819 67 0
11 24 258.266 0.0107348 52 0
12 26 257.181 0.012298 35 0
13 28 256.649 0.00864949 25 0
14 30 256.518 0.00310659 19 0
15 32 256.401 0.00335775 15 0
16 34 256.317 0.00312291 12 0
17 36 256.252 0.00307883 7 0
18 38 256.245 0.000546973 6 0
19 40 256.236 0.000864426 5 0
20 42 256.227 0.0010377 4 0
21 44 256.224 0.000510969 3 0
22 46 256.22 0.000677599 3 0
23 48 256.218 0.000404828 1 0
24 50 256.218 0.000140253 1 0
25 52 256.217 0.000193302 1 0
26 54 256.217 0.00021431 1 0
27 56 256.217 0.000205629 1 0
28 58 256.216 9.93736e-05 5.88e-05 0
Local minimum possible.
lsqnonlin stopped because the final change in the sum of squares relative to
its initial value is less than the selected value of the function tolerance.
% what is the solution?
params
params =
0.260043242623885
% what is the median of the data?
median(x)
ans =
0.260365029783367
% notice that the solution is nearly identical to the median of the data. % (the slop comes from the tolerance used in the optimization and % from the interpolation used in the calculation of the median.)