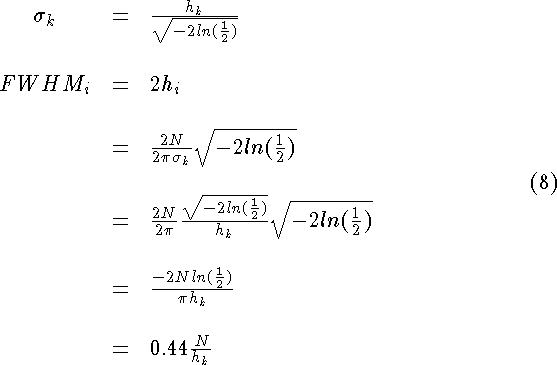If it is desired to reduce high frequency 2D spatial noise, a LPF (Low Passs Filter) can be used by selecting a LPF choice. Then prior to the FFT, the fid image is multiplied by the specified 2D filter.
The K-space gaussian filter has a HWHM (Half Width - Half Maximum) equal to the radius specified in Radius field. The FWHM (Full Width - Half Maximum) is simply equal to twice the radius. The values, g(r), of the gaussian filter are given for one dimension in Equation 1 for a radius = h and an image width of N pixels.
The ![]() for the HWHM radius, h, is
given in Equation 2.
for the HWHM radius, h, is
given in Equation 2.
Multiplication in K-space is equivalent to convolution in Image-space.
Thus the relationship between gaussian filter FWHM in K-space to the FWHM in Image-space can be determined by taking the Fourier Transform (FT) of the K-space gaussian.
But a gaussian with ![]() in the numerator is just another gaussian
with
in the numerator is just another gaussian
with ![]() in the denominator.
in the denominator.
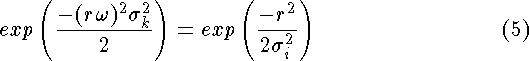
By equating the exponents and replacing ![]() , the Image-space
, the Image-space
![]() can be determined.
can be determined.
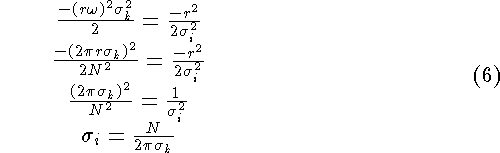
From equation 2 the Image-space HWHM, ![]() , is
, is
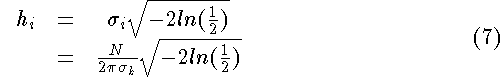
Substituting for ![]() and noting that FWHM = 2h
and noting that FWHM = 2h